Texto
Testes de hipóteses correspondem a procedimentos estatísticos que se baseiam na análise de uma amostra a partir da teoria de probabilidades e que buscam avaliar parâmetros desconhecidos de uma população. Assim, são formuladas duas hipóteses:
- Hipótese nula (H0): hipótese que representa a ausência do efeito que se deseja verificar;
- Hipótese alternativa (H1): hipótese que o investigador deseja verificar.
O teste t nada mais é que um teste de hipóteses que utiliza conceitos estatísticos para que se rejeite ou não uma hipótese nula. É normalmente utilizado quando a variância da população é desconhecida e a estatística do teste segue uma distribuição normal. Se o objetivo é testar se a média da amostra  é estatisticamente diferente, menor ou maior que uma média especificada sob a hipótese nula, μ0, constrói-se o teste utilizando uma ou duas caudas da distribuição t-Student:
é estatisticamente diferente, menor ou maior que uma média especificada sob a hipótese nula, μ0, constrói-se o teste utilizando uma ou duas caudas da distribuição t-Student:
- Se a hipótese nula for
 e a hipótese alternativa
e a hipótese alternativa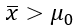 , então devemos usar o teste unicaudal;
, então devemos usar o teste unicaudal; - Se a hipótese nula for
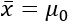 , a hipótese alternativa será
, a hipótese alternativa será  , e devemos usar o teste bicaudal.
, e devemos usar o teste bicaudal.
Assim, no teste bicaudal é preciso considerar as áreas abaixo da curva para valores superiores a t e inferiores a –t, ou seja, as duas caudas. Vale ressaltar que a vantagem de um teste unicaudal sobre um bicaudal é que este teste de uma cauda amplia a região de rejeição, tornando mais fácil rejeitar H0 (mais robusto).
É importante salientar que, em testes de hipóteses, pretendemos aceitar ou rejeitar uma hipótese sobre a média da distribuição. Assim, devemos utilizar o desvio padrão amostral da média,  . A fórmula do teste t é:
. A fórmula do teste t é:

Em que  é a média da amostra, μ0 é a média sob a hipótese nula, s o desvio padrão amostral, n é o tamanho da amostra e
é a média da amostra, μ0 é a média sob a hipótese nula, s o desvio padrão amostral, n é o tamanho da amostra e  é o desvio padrão amostral da média.
é o desvio padrão amostral da média.
Rejeita-se a hipótese nula caso a média amostral for estatisticamente diferente da média da hipótese nula, dado uma confiança desejada. Assim, caso o t calculado seja maior do que o valor t de referência (na tabela) da distribuição, rejeita-se a hipótese nula.
Pode-se dizer que o t calculado é a diferença, em desvios padrão, entre a média amostral e a média sob a hipótese nula. Quanto maior for o t, mais confiante estamos em rejeitar a hipótese nula.
Figura – Testes de hipótese e área de rejeição da hipótese nula.

Fonte: Elaborada pelo autor.
Se o teste for bicaudal e a amostra for suficientemente grande, o valor crítico de t para 5% de significância (ou 95% de confiança) será tα/2 = 1,96 à direita e – tα/2 = -1,96 à esquerda, enquanto que se o teste for unicaudal, o valor crítico para 5% será tα = 1,65 à direita ou – tα = – 1,65 à esquerda.
Premissas do teste de hipóteses:
- a amostra é aleatória (randômica): isso atesta que sujeitos, casos ou eventos de uma determinada população têm a mesma chance de serem selecionados para a pesquisa ou amostra;
- variáveis independentes (independência local): dois eventos não têm nada a ver um com o outro, assim a escolha de um não afeta a escolha do outro;
- a distribuição do que está sendo testado é normal: formato de sino, unimodal e simétrica em relação a sua média.
Erros do Tipo I e Tipo II
Um erro do tipo I consiste em rejeitar uma hipótese nula que é verdadeira, ou seja, encontrar um resultado que tenha significância estatística por acidente. Já um erro do tipo II representa uma falha na rejeição de uma hipótese nula inválida. A taxa de erro tipo I é afetada por α: quanto menor for o nível α, menor será a taxa de erro tipo I. Vale ressaltar que α não é a probabilidade de um erro de tipo I; α é a probabilidade de um erro de Tipo I contanto que a hipótese nula seja verdadeira. Caso a hipótese nula seja falsa, então é impossível fazer um erro de tipo I.
O erro tipo II é o de não rejeitar uma falsa hipótese nula. Diferentemente de um erro de tipo I, um erro de tipo II não é realmente um erro. Quando um teste estatístico não é significativo, isso significa que os dados não fornecem uma forte evidência de que a hipótese nula seja falsa.
A falta de significância não sustenta a conclusão de que a hipótese nula seja verdadeira. Portanto, um pesquisador não deve cometer o erro de concluir incorretamente que a hipótese nula é verdadeira quando um teste estatístico não era significativo. Em vez disso, o pesquisador deve considerar o teste como inconclusivo. Contraste isso com um erro de tipo I no qual o pesquisador conclui erroneamente que a hipótese nula é falsa quando, de fato, é verdadeira. Um erro de tipo II só pode ocorrer se a hipótese nula for falsa. Se a hipótese nula for falsa, a probabilidade de um erro de tipo II é denominada β. A probabilidade de se rejeitar corretamente uma hipótese nula falsa é igual a 1-β.
O quadro abaixo elenca os possíveis cenários:
Quadro - Condição verdadeira.
|
Decisão |
Condição Verdadeira |
|
| H0 é verdadeira | H0 é falsa | |
| Não rejeitar H0 |
Decisão correta |
Decisão incorreta |
| Rejeitar H0 | Decisão Incorreta (Erro tipo I) Nível de significância = α |
Decisão correta Poder do teste = 1-β |
Fonte: Elaborada pelo autor.
Lembrando que: β é o símbolo da probabilidade de um erro do tipo II, assim o poder de um teste estatístico é definido como 1-β. Se realizarmos um teste com alta sensitividade, teremos menos erros do tipo II; porém, se diminui a probabilidade do erro tipo II, aumenta a suscetibilidade do tipo I.
Assim, um nível de significância α de 0,05 (que usualmente é considerado como o patamar para avaliar a hipótese nula) indica que existe uma probabilidade de 5% de rejeitarmos uma hipótese nula quando ela é verdadeira.
Valor-p
O valor-p é a probabilidade de se obter uma estatística do teste (por exemplo, média) que seja igual ou mais extrema que a estatística encontrada na amostra observada, sob a suposição que a hipótese nula é verdadeira. Graficamente, representa a área embaixo da curva após o t calculado.
Se o valor-p é menor que o nível de significância α, rejeita-se a hipótese nula.
Se o valor-p é maior que o nível de significância α, não podemos rejeitar a hipótese nula.
Análise de Variância (ANOVA)
Trata-se de um teste estatístico que se propõe a verificar se existe uma diferença significativa entre as médias, ou seja:
H0: μ1 = μ2 = ... = μk; e
H1: As médias não são iguais.
No caso, existem dois grupos para se calcular a variância: entre grupos (Média quadrada dos grupos - MQG) e dentro dos grupos (Média quadrada dos erros - MQR). A MQG mede a variância das médias, enquanto a MQR mede a variância que existe dentro dos grupos individuais de dados. Dessa forma, são calculados esses dois componentes de variância; caso MQG seja maior que MQR, temos o indicativo de uma diferença significativa entre os grupos.
A ANOVA pode resolver dois problemas: a níveis fixos ou a níveis aleatórios (isso é determinado pela aleatoriedade e, na maioria dos casos, trata-se de níveis fixos).
Tabela - ANOVA.
|
Fonte de variação |
SQ |
GL |
MQ |
Teste F |
|
Entre grupos |
SQG |
K-1 |
MQG |
MQG/MQR |
|
Dentro dos grupos |
SQR |
N-K |
MQR |
|
|
Total |
SQT |
N-1 |
|
|
Fonte: Elaborada pelo autor.
SQT = SQG + SQR (mensura a variação de todas as observações)
SQT: Soma dos quadrados totais
SQG: Soma dos quadrados dos grupos
SQR: Soma dos quadrados dos erros
MQG: Média quadrada dos grupos
MQR: Média quadrada dos erros
SQG e MQG: Medem a variação total das médias
SQR e MQR: Medem a variação das observações de cada grupo
Dessa forma, temos:
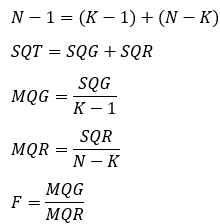
Assim, a hipótese nula será rejeitada quando o F calculado for maior que o valor tabelado, que acontece se a razão entre MQG e MQR seja estatisticamente significante. Por exemplo, se o F tabelado para um intervalo de confiança de 95% for menor que o F calculado, conclui-se que pelo menos uma das médias μ é diferente das outras, e a H0 é rejeitada com α = 0,05.
Simulação de Monte Carlo
A principal ideia por trás da simulação de Monte Carlo é que os resultados são calculados com base em uma amostragem aleatória repetidas vezes, isto é, esse método é uma experimentação aleatória. As simulações de Monte Carlo são caracterizadas por uma grande quantidade de parâmetros desconhecidos e, além disso, alguns poderiam ser difíceis de se obter experimentalmente. Os métodos de simulação de Monte Carlo nem sempre requerem números verdadeiramente aleatórios para serem úteis. Algumas das técnicas mais úteis utilizam sequências deterministas que facilitam a prova e a conferência das simulações com posteriores contraprovas.
Uma simulação do tipo Monte Carlo de qualidade deveria ser capaz de gerar números pseudoaleatórios. Esses valores precisam passar em testes de aleatoriedade, que são comumente disponíveis em diversos softwares de estatística. É preciso utilizar um número de amostras suficientemente grande para que se garanta resultados precisos. Além disso, é necessário que sejam utilizadas técnicas de amostragem adequadas, de modo que o algoritmo usado consiga modelar e simular o fenômeno em estudo.
As simulações de Monte Carlo têm sido utilizadas em diversas áreas da ciência, desde a teoria dos jogos até a biologia computacional. Mas é talvez em finanças que esse método tenha uma de suas maiores aplicações. Ele é comumente usado para avaliar o risco e a incerteza que afetariam o resultado de diferentes opções de mercado, dúvidas sobre investimentos etc. É possível, por exemplo, simplesmente por meio da instalação de uma extensão no Microsoft Excel, realizar simulações de Monte Carlo e, desse modo, permitir que o analista de risco empresarial incorpore os efeitos totais de incerteza, como variáveis incertas do tipo volume de vendas, commodities e preços do trabalho, juros e taxas de câmbio – para o trimestre ou ano seguinte. Simular vários cenários e ver qual seria a situação no futuro para cada um dos cenários fictícios, estipulando, assim, status como “otimista”, “neutro” ou “pessimista”. Além disso, o método é frequentemente usado para avaliar investimentos em projetos em uma unidade de negócios ou a nível corporativo. Sua utilização também é comum para avaliar derivativos financeiros. Uma das utilizações mais comuns do método de Monte Carlo é calcular o preço das opções incorporando análises de risco para diferentes cenários.
A limitação mais importante é o tempo necessário para calcular o grande número de histórias necessárias a fim de reduzir as incertezas estatísticas. Observa-se ainda a necessidade de grande capacidade computacional.
