Texto
Uma regressão linear é normalmente utilizada para análises preditivas e possui como objetivo geral analisar duas coisas: primeiro, um conjunto de variáveis preditoras (capaz de um bom trabalho ao prever uma variável dependente); segundo, quais variáveis em particular são preditores significativos e de que forma elas impactam (magnitude e sinal das estimativas) a variável dependente.
Regressão linear simples
Para um conjunto de dados com duas variáveis (X e Y) o objetivo da regressão é encontrar E(Y | Xi), ou seja, a esperança do valor de Y dado um valor de Xi. A equação que mede o verdadeiro impacto de X em Y é a Função de Regressão Populacional (FRP), que é dada por E(Y | Xi) = α + β*Xi. Como trabalhamos com amostras na maioria das vezes, temos somente estimativas de α e β, chamadas de 'α chapéu' e 'β chapéu'. Assim, a equação da reta de uma Função de Regressão Amostral (FRA) é dada por:
Em que:
- Y é a variável dependente e
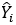é o valor predito de Y dado um Xi; - X é a variável independente;
-
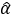é o valor previsto de Y quando X = 0 (o intercepto); e -
é o quanto Y muda, em média, por unidade de mudança em X (a inclinação).
Assim, a inclinação ou coeficiente de regressão (β) mede a direção ou magnitude da relação, de forma que se as duas variáveis estão correlacionadas positivamente, a inclinação será positiva e vice-versa.
O conjunto de dados muito provavelmente não mostrará uma relação exata entre X e Y. Isso porque (1) é possível ter outros fatores que afetam Y além de X, e (2) a variância da amostra cria uma dispersão nos dados, fazendo que amostras diferentes tenham FRAs diferentes. Assim, podemos representar a FRA em sua forma estocástica da seguinte forma:
Em que 
representa o resíduo da regressão (amostral) para a observação i. O erro é o termo que inclui todos os fatores que determinam Y e não são explicados por X, e o resíduo pode ser considerado a estimativa do erro.
Exemplo: Considere as seguintes amostras de X e Y:
Tabela - Amostras de X e Y.
| X | 4 | 6 | 7 | 5 | 8 | 10 |
| Y | 15 | 18 | 19 | 20 | 21 | 23 |
Fonte: Elaborada pelo autor.
Colocando estes pontos em um gráfico, podemos ver que eles estão dispersos e não formam uma linha reta. O objetivo da regressão linear é encontrar o intercepto e a inclinação de uma reta que melhor ajuste a estes dados, ou seja, que minimize a variância dos erros, e, portanto, nos gere a melhor estimativa de α e β. A reta que realiza este objetivo é encontrada pela técnica de mínimos quadrados, por meio da minimização da soma dos quadrados dos resíduos. A reta encontrada pelos Mínimos Quadrados Ordinários (MQO ou Ordinary Least Squares - OLS) da amostra é a seguinte:
Figura - Regressão linear simples.
Fonte: Elaborado pelo autor
Como o β estimado é igual a 1,24, podemos dizer que, em média, quando X muda 1 unidade, Y varia em 1,24 unidades.
Cada observação i pode ser resumida em uma fórmula que relaciona Yi com a reta mais um resíduo. Utilizando os dados acima, temos:
A variável dependente (Y) pode ser chamada de variável de resultado, variável de critério ou variável endógena. Já as variáveis independentes (X) também podem ser chamadas de variáveis exógenas, preditoras ou regressores.
As fórmulas de β e α podem ser encontradas pelas covariâncias, variâncias e valores médios de X e Y:
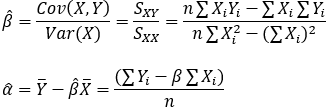
Em que Sxx e Sxy são as somas dos quadrados de X e soma dos desvios de X e Y, respectivamente:
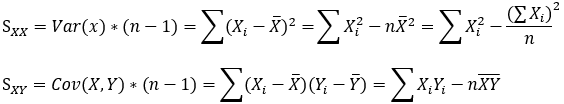
Coeficiente de determinação (R²)
O coeficiente de correlação (R), que varia de -1 a 1, é o que fará a mensuração da relação linear entre as duas variáveis. Um R igual a 1 indica correlação perfeita; o oposto, forte correlação negativa. Já valores próximos a zero indicam fraca correlação.
Também é importante considerar, na interpretação dos dados, o cálculo Coeficiente de Determinação (R²), que é uma medida de ajustamento que varia de 0 a 1, indicando, em porcentagem, o quanto o modelo consegue explicar os valores observados. Assim, quanto maior o R², mais explicativo é o modelo e melhor ele se ajusta à amostra.
Uma maneira de calcular o R² é por meio das somas dos quadrados totais, dos resíduos e explicados (SQT, SQR e SQE):
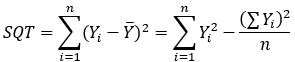
SQT é a soma dos quadrados totais; n o número de observações; Yi o valor observado; e Ȳ é a média de observações. A equação, então, nos fornece a soma dos quadrados das diferenças entre a média e cada valor observado.
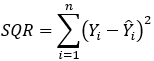
SQR é a soma dos quadrados dos resíduos, que calcula a parte não explicada do modelo, e 
é o valor estimado (previsão) de Yi.
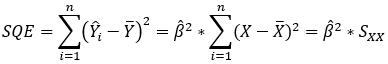
SQE é a soma dos quadrados explicados, que indica a diferença entre a média das observações e o valor estimado para cada observação, e soma os respectivos quadrados. Assim, quanto menor for a diferença, maior poder explicativo o modelo possui.
Como R² é o percentual que o modelo (α + β*X) explica a variação total (Y), R² = SQE/SQT. E como SQT = SQE + SQR, também podemos calcular o R² da seguinte forma:
Outra forma de calcular o R² é calculando o R:
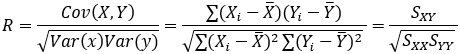
e elevando o resultado ao quadrado.
O R² possui uma capacidade de encontrar a probabilidade de eventos futuros dentro dos resultados previstos. Assim, caso mais amostras sejam adicionadas, o coeficiente mostrará a probabilidade de um novo ponto cair na linha estimada pela regressão. Mesmo se houver uma forte conexão entre as duas variáveis, a determinação não provará causalidade. Por exemplo, um estudo sobre aniversários que mostra que um grande número de aniversários acontece dentro de um período em determinado mês não significa que a passagem do tempo ou a mudança das estações do ano influencie na ocorrência de gravidez.
Regressão linear múltipla
A equação é dada por Y = β0 + β1X1 + β2X2 + … + βkXk + ε, em que ε é o erro aleatório. Obviamente, quando acrescentamos mais variáveis dentro de uma equação, surgem mais problemas visto que a variável dependente acaba condicionada a valores de n fatores. Os princípios seguem o mesmo da regressão simples vista anteriormente, porém o analista deve se preocupar com o R², que indica a variabilidade total do modelo de regressão.
É importante, contudo, que se tenha cuidado ao adicionar variáveis desnecessárias ao modelo, pois pode ocorrer o que é chamado de overfitting, o que reduz a generalização do modelo. Assim, quanto mais simples, melhor. A Navalha de Occam descreve o problema extremamente bem: um modelo simples é geralmente preferível a um modelo mais complexo. Estatisticamente, se um modelo inclui um grande número de variáveis, algumas das variáveis serão estatisticamente significativas devido ao acaso. A rejeição da hipótese nula continua a mesma: a rejeição ocorre caso o valor calculado seja maior que o valor tabelado.
Correlação/autocorrelação
Como vimos, o valor de um coeficiente de correlação varia de -1 até 1. Um valor de -1 indica uma correlação negativa perfeita, enquanto um valor de 1 indica uma correlação positiva perfeita. Uma correlação de zero significa que não há relação entre as duas variáveis. Quando há uma correlação negativa entre duas variáveis, conforme o valor de uma variável aumenta, o valor da outra variável diminui e vice-versa. Ou seja, para uma correlação negativa, as variáveis trabalham uma em frente da outra. Quando há uma correlação positiva entre duas variáveis, conforme o valor de uma variável aumenta, o valor da outra variável também aumenta, já que as variáveis se movem juntas. A probabilidade da estatística-t indica se o coeficiente de correlação observado ocorreu por acaso quando a correlação verdadeira for zero. Em outras palavras, questiona se a correlação é significativamente diferente de zero.
Assim, se E(εiεj) ≠ 0, para i,j = 1, 2, 3…, então o valor de um resíduo passa a influenciar os resultados futuros da média condicional estimada para Y, trazendo o problema de autocorrelação serial. Dentre as principais fontes de correlação, podemos citar: omissão de variável relevante, má especificação funcional ou dinâmica do modelo.
Um dos pressupostos básicos da regressão linear é de que o termo residual é distribuído de forma independente e também os resíduos não são correlacionados entre si. A autocorrelação viola esse pressuposto. Assim, caso haja presença de autocorrelação, é importante que se use um modelo autorregressivo, pois é mais adequado para o caso.
Teste t em um coeficiente de regressão
Para realizar testes de hipóteses no coeficiente de regressão de uma regressão linear simples, utilizamos o mesmo conceito para testes em médias. O teste é dado por:
Onde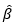 
é o β estimado pela amostra, β0 é uma constante definida pelo teste desejado e 
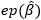é o erro padrão do β estimado.
Para testar a significância do teste, testamos a hipótese nula de que não há correlação entre X e Y, e portanto, neste caso, nossa constante β0 é igual a zero.
Estatística F
A estatística F é usada para testar a hipótese de todos os coeficientes de regressão, exceto a constante. É útil quando nosso modelo possui mais de uma inclinação. Nossa hipótese nula H0 é β1 = β2 = … = βk = 0 e a hipótese alternativa é que nem todos os β são igual a 0. Ela pode ser escrita em função da soma dos quadrados:
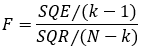
Ou, alternativamente, em função do R²:
Em que k é a quantidade de coeficientes na regressão (incluindo o intercepto). Considerando a ideia de que os resíduos teóricos possuem distribuição normal, essa estatística tem distribuição F com (k-1) graus de liberdade e (N-k) graus de liberdade no denominador. Para testar a hipótese nula, usa-se o nível de significância associado à estatística F (se for menor do que 5%, podemos rejeitar a hipótese nula).
Exercício 1
Dado um experimento em que se analisa a octanagem da gasolina (Y) em função da adição de um novo aditivo (X) e no qual foram realizados ensaios com percentuais de 1% até 6% de aditivo. Considerando os resultados a seguir, calcule a reta de regressão.
Tabela - Resultados.
| X (%) | 1 | 2 | 3 | 4 | 5 | 6 |
| Y | 80, 5 | 81,6 | 82,1 | 83,7 | 83,9 | 85,0 |
Fonte: Elaborada pelo autor.
Resolução:
A estimativa da reta é E(Y) = α + βx, na qual α e β são os parâmetros do modelo.
Para obtermos a equação, é preciso criar uma tabela com os cálculos:
Tabela - Dados e cálculos.
| Dados | Cálculos | |||
| i | Xi | Yi | Xi2 | XiYi |
| 1 | 1 | 80,5 | 1 | 80,5 |
| 2 | 2 | 81,6 | 4 | 163,2 |
| 3 | 3 | 82,1 | 9 | 246,3 |
| 4 | 4 | 83,7 | 16 | 334,8 |
| 5 | 5 | 83,9 | 25 | 419,5 |
| 6 | 6 | 85,0 | 36 | 510 |
| Soma | 21 | 496,8 | 91 | 1754,3 |
Fonte: Elaborada pelo autor.
Aplicando os resultados obtidos na fórmula de β e α estimados, temos:
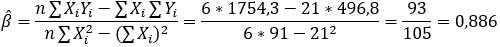
Assim, temos a reta da equação:
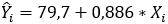
Exercício 2
Espera-se que a massa muscular de uma pessoa diminua à medida que a idade aumenta. Para estudar essa relação, uma nutricionista selecionou 18 mulheres, com idade entre 40 e 79 anos, e observou em cada uma delas a idade (X) e a massa muscular (Y).
Tabela - Dados do Exercício 2.
| i | Massa Muscular (Y) | Idade (X) | i | Massa Muscular (Y) | Idade (X) |
| 1 | 82,0 | 71,0 | 10 | 84,0 | 65,0 |
| 2 | 91,0 | 64,0 | 11 | 116,0 | 45,0 |
| 3 | 100,0 | 43,0 | 12 | 76,0 | 58,0 |
| 4 | 68,0 | 67,0 | 13 | 97,0 | 45,0 |
| 5 | 87,0 | 56,0 | 14 | 100,0 | 53,0 |
| 6 | 73,0 | 73,0 | 15 | 105,0 | 49,0 |
| 7 | 78,0 | 68,0 | 16 | 77,0 | 78,0 |
| 8 | 80,0 | 56,0 | 17 | 73,0 | 73,0 |
| 9 | 65,0 | 76,0 | 18 | 78,0 | 68,0 |
Fonte: Elaborada pelo autor.
a. Calcule o coeficiente de correlação linear R entre X e Y.
b. Calcule a reta de regressão para a relação entre as variáveis Y: massa muscular (dependente) e X: idade (independente).
c. Estime a massa muscular média de mulheres com 50 anos.
Resolução:
a.
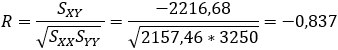
r = -0,837, o que significa que há uma forte correlação linear negativa entre a variável massa muscular e idade.
b.
O β e α estimados do modelo são:
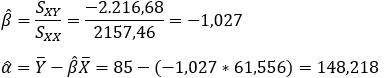
Portanto, a reta de regressão estimada da variável massa muscular (Y) em função da idade (X) é:
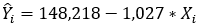
c.
Para encontrar a estimativa da massa muscular média para mulheres com 50 anos, basta substituir os valores de X para o caso em que X = 50 na equação que obtivemos acima:
Exercício 3
(FCC Analista BACEN 2005) Uma empresa com a finalidade de determinar a relação entre os gastos anuais com propaganda (X), em R$ 1000,00, e o lucro bruto anual (Y), em R$ 1000,00, optou por utilizar o modelo linear simples Y(i) = a + bX(i) + e(i), em que Y(i) é o valor do lucro bruto auferido no ano (i), X(i) é o valor do gasto com propaganda no ano (i) e e(i) o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Considerou, para o estudo, as seguintes informações referentes às observações dos últimos 10 anos da empresa:
∑Yi = 100; ∑Xi = 60; ∑YiXi= 650; ∑Xi2 = 400; e ∑Yi2 = 1080.
Montando o quadro de análise de variância (ANOVA), encontre:
- a variação total (SQT);
- a variação explicada, fonte de variação devido à regressão (SQE);
- a variação residual (SQR).
Resolução:
Sendo assim, a variação total é 80, a explicada é 62,5 e a residual apresenta um valor igual a 17,5.
Exercício 4
(SUSEP 2010 modificada) A partir de uma amostra aleatória [x(1), y(1)], [x(2), y(2)]...[x(20), y(20)], foram obtidas as estatísticas:
Média de X = 12,5;
Média de Y = 19;
Variância de X = 30;
Variância de Y = 54; e
Covariância entre X e Y = 36.
- Calcule a reta de regressão estimada de Y contra X.
- Determine o valor da estatística F para testar a hipótese nula de que o coeficiente angular da reta do modelo de regressão linear simples de Y contra X é igual a zero. Considere que, com um intervalo de confiança de 95%, o F tabelado é 4,414.
Resolução:
a.
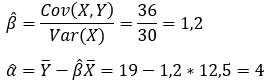
Sendo assim, a reta é igual a:
b.
A partir das variâncias de X e Y e da estimativa do parâmetro β, podemos encontrar as somas dos quadrados:
Considerando que k = 2 (um intercepto + uma inclinação) e n = 20, podemos calcular o F da seguinte maneira:
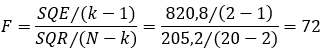
O valor da estatística F é igual a 72. Como 72 > 4,414, rejeitamos a hipótese nula de que todos os β estimados são igual a zero com 95% de confiança. Nesta regressão há somente um β, e, portanto, o teste mostra que a inclinação desta regressão linear simples é estatisticamente significante para um nível de significância de 5%.
Limitações da análise de regressão
Sabemos que a regressão é um modelo estatístico que permite examinar a relação entre uma variável dependente e uma ou mais variáveis independentes. A regressão linear analisa apenas relações lineares entre as variáveis dependentes e independentes, o que pressupõe que exista uma relação direta entre eles e isso nem sempre está correto.
A regressão linear analisa uma relação entre a média da variável dependente e as variáveis independentes, e como a média não se constitui como uma descrição completa de uma única variável, a regressão linear também não é uma descrição completa da relação entre as variáveis. Vale ressaltar que no caso da regressão linear os dados devem ser independentes. A análise de regressão necessita de fortes suposições como a normalidade, independência e homocedasticidade dos erros, sendo essas suas principais limitações.
