Cálculo do Modelo CAPM

Retorno esperado do mercado

O retorno esperado do mercado pode ser representado como:

Ou seja, o retorno esperado do mercado (Rm) é a soma da taxa sem risco (Rf) mais uma remuneração pelo risco inerente da carteira de mercado (prêmio de risco).

Remuneração pela espera e pelo risco

O retorno mínimo esperado sobre o capital próprio investido no negócio considera dois elementos: a remuneração pela espera e a remuneração pelo risco.

A remuneração pela espera é a remuneração justificada pelo sacrifício do consumo presente em troca de um benefício superior no futuro. Essa remuneração considera como referência a taxa de juros oferecida por um investimento livre de risco. No Brasil, sob o ponto de vista do investidor pessoa física, a caderneta de poupança ou títulos públicos são considerados investimentos livres de risco. Portanto, a remuneração oferecida por esse ativo se justifica apenas pela espera.

A remuneração pelo risco é formada por um risco total, o qual é a soma de duas partes: risco diversificável + risco não diversificável. O risco diversificável representa a parcela do risco de um ativo que está associado a um ativo específico e pode ser eliminado através de um portfólio composto por diversos ativos. Ele é representado por eventos específicos, como greves, processos trabalhistas, ações regulatórias, perda de um cliente importante, falta de suprimento de matérias-primas etc.

Quando construímos uma carteira de ativos da mesma natureza (participações acionárias, por exemplo), podemos, através da diversificação entre 15 ou 20 ações, eliminar o risco diversificável. Além disso, uma carteira composta por cinco ativos pode ser mais diversificada que uma outra composta por 10. Isso se justifica pelo fato de a diversificação estar ligada à baixa correlação entre os ativos. Por exemplo, uma carteira composta de 10 ações do mesmo setor tem mais chances de ser afetada por elementos comuns que impactam igualmente todas as empresas daquele setor específico; já em uma carteira composta de cinco ações de setores distintos, esse risco é mitigado.

O risco não diversificável é atribuído a fatores de mercado que afetam todas as empresas e não pode ser eliminado através da diversificação. Fatores como guerra, inflação, crises internacionais e crises políticas são exemplos desse risco.

Através da diversificação, supõe-se que todo investidor possa eliminar todos os riscos diversificáveis. Portanto, o único risco relevante é o não diversificável. Nesse contexto, pesquisas demonstram que investidores são recompensados por assumirem somente aqueles riscos que não podem ser eliminados através da diversificação. Todavia, o investidor deve estar preocupado em eliminar o risco diversificável que reflita a contribuição de um ativo para o risco da carteira.

Coeficiente beta

O coeficiente beta (β) é utilizado para medir o risco não diversificável. Ele mede a sensibilidade dos retornos de um ativo em relação a variações nos retornos do mercado. O retorno de mercado é o retorno da carteira de mercado com todas as ações negociadas.

No Brasil, esse retorno poderá ser medido pela variação do índice Bovespa, que mensura a variação de uma carteira teórica de ações negociadas na Bolsa de Valores de São Paulo (principal bolsa brasileira). Comumente, os coeficientes betas movimentam-se na mesma direção do índice de mercado. Veja a seguir:

Em que:

COVi,m = covariância entre o ativo i e o mercado;
σ2M = variância do mercado;
σi = desvio-padrão do ativo i;
σm = desvio-padrão do mercado; e
ρi,m = coeficiente de correlação entre o ativo i e o mercado.

O beta pode assumir uma série de valores, e sua interpretação é a seguinte:

Se β > 1, reflete um risco sistêmico mais alto que o mercado, sendo que, por isso, é considerado um investimento agressivo; em outras palavras, a carteira de ativos oscila mais que a carteira de mercado;
Se β = 1, a carteira de ativos tem o mesmo risco que a carteira de mercado, movimentando-se na mesma direção;
Se 0 < β < 1, a carteira de ativos é menos arriscada do que a carteira de mercado e o ativo se caracteriza por ser mais defensivo;
Se β < 0, o ativo move-se em direção oposta à do mercado.

Observe o gráfico abaixo, que representa a ideia exposta:

Gráfico - Retorno esperado do título.

Fonte: Retirado de Ross et al. (2007).

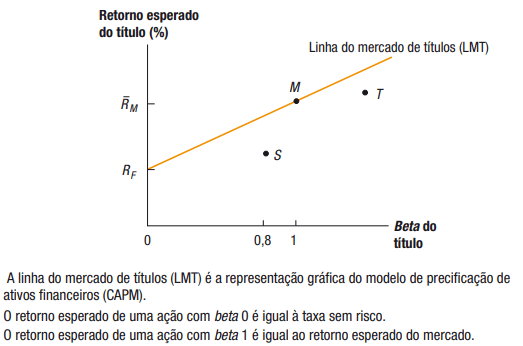
Cálculo do Modelo CAPM

O CAPM é um modelo de formação de preços de ativos que equaciona a relação básica entre risco e retorno, presente em todas as formas de decisões financeiras. Esse modelo também possibilita a estima da taxa de retorno exigida pelos investidores, ou seja, a taxa mínima de atratividade pelo capital próprio.

Uma vez que o risco diversificável pode ser eliminado, o CAPM equaciona a relação entre risco não diversificável e a sua remuneração, ou seja, o prêmio pelo risco. Vale lembrar que entendemos como risco diversificável aquele que pode ser mitigado ao montar um portfólio de ativos.

Segundo o CAPM, o custo de capital corresponde à taxa de rentabilidade exigida pelos investidores como forma de compensação pelo risco de mercado ao qual estão expostos. O CAPM também considera que, em um mercado competitivo, o prêmio de risco varia proporcionalmente ao β, que é justamente a medida de risco não diversificável.

Como em todos os modelos financeiros, formulam-se algumas hipóteses para seu desenvolvimento. São elas:

há uma grande eficiência informativa do mercado, a qual atinge igualmente todos os investidores;
não há impostos, taxas ou quaisquer outras restrições para os investimentos no mercado, sendo ele perfeitamente competitivo;
há uma mesma percepção por parte de todos os investidores quanto ao desempenho dos ativos, formando carteiras eficientes a partir de expectativas idênticas; e
existe uma taxa de juros de mercado definida como livre de risco, e todos os indivíduos podem emprestar e tomar emprestado à mesma taxa.

O modelo CAPM foi elaborado como resposta à seguinte pergunta: qual é o prêmio que faz com que o investidor seja indiferente entre investir em um ativo com risco ou em outro que seja livre de risco? Sharpe (1964) e Lintner (1965) provaram que existe uma relação linear, mensurada por um parâmetro β, entre o excesso de retorno de um investimento e o excesso de retorno do mercado. Assim, o modelo CAPM consiste na seguinte lógica: quanto maior for o coeficiente (βi), que multiplica o prêmio, maior será a sensibilidade do ativo a variações de mercado. Desse modo, maiores serão o risco e a remuneração esperada do ativo.

Observe a seguinte equação:

Em que:

é a taxa de retorno do investimento;
é a taxa média de retorno do mercado; e
é a taxa de retorno do ativo livre de risco.

A equação anterior pode ser reescrita da seguinte forma:

Isto é, o retorno do ativo é igual ao retorno do ativo livre de risco mais o excesso de retorno do mercado em relação ao ativo livre de risco ponderado pelo parâmetro beta. Sendo assim, o CAPM mostra o retorno esperado de um ativo que resulta em equilíbrio no mercado, de modo que não permite a realização de arbitragem.

Sua equação é:

Em que:

Ki é o retorno esperado do ativo i;
rf é o retorno esperado da taxa livre de risco;
βi é a sensibilidade ao risco de mercado;
rm é o retorno histórico do mercado de ações; e
(rm - rf) é o prêmio de risco dos ativos de mercado sobre os ativos livres de risco.

No CAPM, o retorno esperado de um investimento é explicado pelo coeficiente de risco do próprio ativo βi, pela taxa de juros livre de risco Rf (considerada uma taxa de juros para ativos cujos retornos não variam ao longo do tempo, como, por exemplo, a TR ou Selic) e por um prêmio pelo risco de mercado [E (Rm) - Rf]. Esse prêmio pelo risco é a diferença do retorno de um investimento em uma carteira que representa o mercado (geralmente um índice de ações) em relação ao investimento em uma taxa livre de risco.

O coeficiente beta mensura o risco sistemático do mercado. Quando o beta é igual a zero, significa que a rentabilidade de um ativo não varia com a rentabilidade do mercado, de modo que esse ativo pode ser considerado livre de risco. Quando o beta da empresa é igual a 1 (um), o risco do ativo é igual ao risco do mercado. Desse modo, conforme o valor de beta se eleva, o risco sistemático do ativo também aumenta, o que faz com que os acionistas exijam uma remuneração mais elevada. Isso significa que um ativo com risco sistemático superior a 1 (um) apresenta risco sistemático superior ao mercado; por sua vez, um ativo com beta inferior a 1 (um) apresenta risco sistemático inferior ao mercado.

Limitações do CAPM no Brasil

A aplicação do CAPM no Brasil é prejudicada por diversos fatores, tais como:

O retorno livre de risco (rf ) variou enormemente nos últimos anos devido à política econômica do governo;
O beta β e o retorno de mercado (rm) apresentam grande volatilidade em razão de o mercado de capitais ser imperfeito no Brasil devido aos seguintes aspectos:
- pouco volume transacionado;
- poucas ações;
- mercado muito concentrado; e
- empresas que possuem má comunicação com o mercado, o que dificulta a correta avaliação dos ativos.

Reta característica de um ativo

A reta característica de um ativo nada mais é do que uma regressão linear que busca plotar em um gráfico a relação entre o retorno de um ativo e o retorno do mercado. No gráfico da reta característica, o eixo Y representa o 'excesso de retorno do ativo', ou seja, a parcela do retorno do ativo que supera a taxa livre de risco, e o eixo X representa o 'excesso de retorno do mercado', ou seja, a parcela de retorno do mercado que supera a taxa livre de risco.

A reta característica de um ativo tem a seguinte equação geral:

Em que:

Ri é o excesso de retorno do ativo (retorno do ativo - Rf);
αi é o intercepto ou o retorno do ativo quando o retorno do mercado é zero;
βi é o beta do ativo;
RM é o excesso de retorno do mercado (retorno do mercado - Rf); e
ei é o erro presente na regressão.

Veja o gráfico abaixo, o qual representa a reta característica de dois ativos:

Gráfico - Reta característica de dois ativos.

Fonte: Elaborado pelo autor.

A presença do erro na equação ocorre porque a origem da reta característica é uma regressão linear, um estudo empírico estatístico, e, portanto, há variações nos ativos que não podem ser explicadas pela equação teórica. No entanto, foquemo-nos nos aspectos mais relevantes da reta: seu intercepto e sua inclinação. O intercepto nada mais é do que o retorno do ativo quando o retorno do mercado é zero, ou, em termos algébricos, quando igualamos o X a zero (que, neste caso, seria RM=0). A sua inclinação é o beta. Em outras palavras, se tivermos a reta característica de um ativo, será possível obter o seu beta. Desse modo, quanto mais inclinada for a reta característica de um ativo, maiores serão o risco sistemático e o excesso de retorno.

Através das retas características dos ativos acima, podemos afirmar que o ativo A possui maior risco, e, por essa razão, sua remuneração em relação ao mercado é maior, já que o beta é um multiplicador do prêmio pelo risco sistemático. Apesar disso, quando os retornos do mercado estão muito baixos ou são iguais a zero, o ativo B apresenta um retorno mais elevado.

Uma aplicação da reta característica ocorreria se o investidor, ao observar o gráfico acima, chegasse à conclusão de que, em momentos de pouco retorno, ele poderia reduzir seus riscos e ter retornos maiores com o ativo B, substituindo-o pelo ativo A apenas em momentos de euforia dos mercados, pois, nesse caso, o retorno mais elevado poderia justificar a maior tomada de risco (escolha do ativo de maior inclinação, com beta maior).